Stochastic variational learning in recurrent spiking networks

Posted on by

This week we discussed Stochastic variational learning in recurrent spiking networks by Danilo Rezende and Wolfram Gerstner.

Introduction

This paper brings together variational inference (VI) and biophysical networks of spiking neurons. The authors show:

  1. variational learning can be implemented by networks of spiking neurons to learn generative models of data,
  2. learning takes the form of a biologically plausible learning rule, where local synaptic learning signals are augmented with a global “novelty” signal.

One potential application the authors mention is to use this method to identify functional networks from experimental data. Through the course of the paper, some bedrock calculations relevant to computational neuroscience and variational inference are performed. These include computing the log likelihood of a population of spiking neurons with Poisson noise (including deriving the continuum limit from discrete time) and derivation of the score function estimator. I’ve filled in some of the gaps in these derivations in this blog post (plus some helpful references I consulted) for anyone seeing this stuff for the first time.

Neuron model and data log likelihood

The neuron model used in this paper is the spike response model which the authors note (and we discussed at length) is basically a GLM. The membrane potential of each unit in the network is described by the following equation:

\mathbf{u} = \mathbf{w \phi(t)} + \mathbf{\eta(t)}

where ​\mathbf{u} is a N​-dimensional vector, ​\mathbf{\phi}(t) are exponentially filtered synaptic currents from the other neurons, w is a N \times N matrix of connections and ​\mathbf{\eta}(t) is an adaptation potential that mediates the voltage reset when a neuron spikes (this can be thought of as an autapse).

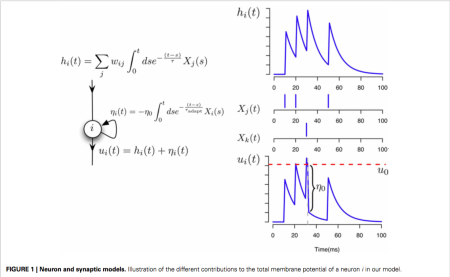
Figure1

Spikes are generated by defining an instantaneous firing rate ​\rho(t) = \rho_0 \text{exp}[\frac{\mathbf{u} - \theta}{\Delta u}] where \theta, \Delta u and \rho_0 are physical constants. The history of all spikes from all neurons ​is denoted by \mathbf{X}. We can define the probability the ​i^{th} neuron producing a spike in the interval ​[t,t+\Delta t], conditioned on the past activity of the entire network ​\mathbf{X}(0...t) as P_i(t_i^f \in [t,t+\Delta t] | \mathbf{X}(0...t)) \approx \rho_i(t) \Delta t, and the probability of not producing a spike as ​P_i(t_i^f \notin [t,t+\Delta t] | \mathbf{X}(0...t)) \approx 1 - \rho_i(t) \Delta t.

Aside: in future sections, the activity of some neurons will be observed (visible) and denoted by a super- or subscript ​\mathcal{V} and the activity of other neurons will be hidden and similarly denoted by ​\mathcal{H}. 

We can define the joint probability of the entire set of spikes as: 

P(X(0...T)) \approx \Pi_{i \in \mathcal{V} \cup \mathcal{H}} \Pi_{k_i^s} [\rho_i(t^f_{k_i^s})\Delta t] \Pi_{k_i^{ns}} [1 - \rho_i(t^f_{k_i^{ns}})\Delta t]

The authors re-express this in the continuum limit. A detailed explanation of how to do this can be found in Abbott and Dayan, Chapter 1, Appendix C. The key is to expand the log of the “no spike” term into a Taylor series, truncate at the first term and then exponentiate it:

​\text{exp} \hspace{1mm} \text{log} (\Pi_{k_i^{ns}} [1 - \rho_i(t^f_{k_i^{ns}})\Delta t]) = \text{exp} \sum_{k_i^{ns}} \text{log} [1 - \Delta t \rho_i(t_{k_i^{ns}}^f)] \approx \text{exp} \sum_{k_i^{ns}} - \Delta t \rho_i(t_{k_i^{ns}}^f).

As ​\Delta t \rightarrow 0, this approximation becomes exact and the sum across bins with no spikes becomes an integral across time, 

P(\mathbf{X}(0...T)) = \Pi_{i \in \mathcal{V} \cup \mathcal{H}} [\Pi_{t_i^f}\rho_i(t_i^f) \Delta t] \text{exp}(- \int_0^T dt \rho_i(t))

from which we can compute the log likelihood,

\text{log} P(\mathbf{X}(0...T) = \sum_{i \in \mathcal{V} \cup \mathcal{H}} \int_0^T d\tau [\text{log} \rho_i(\tau) \mathbf{X}_i(\tau) - \rho_i(\tau)]

where we use ​\mathbf{X}_i(\tau) to identify the spike times.

They note that this equation is not a sum of independent terms, since ​\rho depends on the entire past activity of all the other neurons.

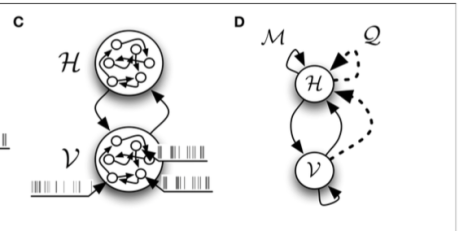
Figure2

Figure 2 from the paper show the relevant network structures we will focus on. Panel C shows the intra- and inter- network connectivity between and among the hidden and visible units. Panel D illustrates the connectivity for the “inference” ​\mathcal{Q} network and the “generative” ​\mathcal{M} network. This structure is similar to the Helmholtz machine of Dayan (2000) and the learning algorithm will be very close to the wake-sleep algorithm used there.

Variational Inference with stochastic gradients

From here, they follow a pretty straightforward application of VI. I will pepper my post with terms we’ve used/seen in the past to make these connections as clear as possible. They construct a recurrent network of spiking neurons where the spiking data of a subset of the neurons (the visible neurons or “the observed data”) can be explained by the activity of a disjoint subset of unobserved neurons (or a “latent variable” ala the VAE). Like standard VI, they want to approximate the posterior distribution of the spiking patterns of the hiding variables (like one would approximate the posterior of a latent variable in a VAE) by minimizing the KL-divergence between the true posterior and an approximate posterior q:

KL(q;p) = \int \mathcal{D} \mathcal{X_H} q(\mathcal{X_H} | \mathcal{X_V}) \text{log} \frac{q(\mathcal{X_H} | \mathcal{X_V})}{p(\mathcal{X_H} | \mathcal{X_V})}

= \langle \text{log} q(\mathcal{X_H} | \mathcal{X_V}) - \text{log} p(\mathcal{X_H,X_V}) \rangle_{q(\mathcal{X_H} | \mathcal{X_V})} + \text{log} p(\mathcal{X_V})

= \langle \mathcal{L^Q} - \mathcal{L^M} \rangle_{q(\mathcal{X_H} | \mathcal{X_V})} + \text{log} p(\mathcal{X_V}).

The second term is the data log likelihood. The first term, ​\mathcal{F}, is the Helmholtz free energy and like always in VI it represents an upper bound on the negative log likelihood. We can therefore change our optimization problem to minimize this function with respect to the parameters of ​q (the approximate posterior) and p (the true posterior)​. We do this by computing the gradients of ​\mathcal{F} with respect to the ​\mathcal{Q} (inference) network and the \mathcal{M} (generative) network​. First, the \mathcal{M} network, since it’s easier:

​\dot{w_{ij}^\mathcal{M}} = -\mu^\mathcal{M} \nabla_{w_{ij}^\mathcal{M}} \mathcal{F} = \mu^\mathcal{M} \nabla_{w_{ij}^\mathcal{M}} \langle \mathcal{L^Q} - \mathcal{L^M} \rangle_q = \mu^\mathcal{M} \langle \nabla_{ij}^\mathcal{M} \mathcal{L^M} \rangle_q \approx \mu^\mathcal{M} \nabla_{w_{ij}^\mathcal{M}} \hat{\mathcal{L}}^\mathcal{M}

where ​\hat{\mathcal{L}}^\mathcal{M} is a point estimate of the complete data log likelihood of the generative model. They will compute this with a Monte Carlo estimate. The gradient of the complete data log likelihood with respect to the connections is:

\nabla_{w_{ij}^\mathcal{M}} \hat{\mathcal{L}}^\mathcal{M} = \nabla_{w_{ij}^\mathcal{M}} \text{log} p(\mathcal{X_H, X_V}) = \sum_{k \in \mathcal{V} \cup \mathcal{H}} \int_0^T d\tau \frac{\partial \text{log} \rho_k(\tau)}{\partial w_{ij}^\mathcal{M}} [\mathbf{X}_k(\tau) - \rho_k(\tau)]​.

Here they used the handy identity: \frac{\partial f(x)}{\partial x} = \frac{\partial[\text{log} f(x)]}{\partial x} f(x)​. 

The derivative of the firing rate function can be computed with the chain rule, \frac{\partial [\text{log} \rho_k(\tau)]}{\partial w_{ij}^\mathcal{M}} = \delta_{ki} \frac{g^\prime(u_k(\tau))}{g(u_k(\tau))} \phi_j(\tau).

This equation for updating the weights using gradient ascent is purely local, taking the form of a product between a presynaptic component, ​\phi_j(\tau), and a postsynaptic term ​\frac{g^\prime(u_k(\tau))}{g(u_k(\tau))} [\mathbf{X}_k(\tau) - \rho_k(\tau)]​.

They also compute the gradient of ​\mathcal{F} with respect to the ​\mathcal{Q} network, ​-\mu^\mathcal{Q} \nabla_{w_{ij}^\mathcal{Q}} \mathcal{F}. To do this, I revisited the 2014 Kingma and Welling paper, where I think they were particularly clear about how to compute gradients of expectations (i.e. the score function estimator). In section 2.2 they note that:

​\nabla_\phi \langle f(z) \rangle_{q_\phi (z)}= \langle f(z) \nabla_\phi \text{log} q_\phi (z) \rangle .

A cute proof of this can be found here. This comes in handy when computing the gradient of ​\mathcal{F} with respect to the connections of the \mathcal{Q} network:

​\nabla_{w_{ij}^\mathcal{Q}} \mathcal{F} = \langle \mathcal{F} \nabla_{w_{ij}^\mathcal{Q}} \text{log} q(\mathcal{X_H} | \mathcal{X_V}) \rangle = \langle \mathcal{F} \nabla_{w_{ij}^\mathcal{Q}} \mathcal{L^Q} \rangle \approx \hat{\mathcal{F}} \nabla_{w_{ij}^\mathcal{Q}} \hat{\mathcal{L}}^\mathcal{Q}.

Here again we compute Monte Carlo estimators of ​\mathcal{F} and \mathcal{L^Q}. ​\nabla_{w_{ij}^\mathcal{Q}} \hat{\mathcal{L}}^\mathcal{Q} takes the exact same form as for the ​\mathcal{M} network, but the neat thing is that ​\nabla_{w_{ij}^\mathcal{Q}} \mathcal{F} contains a term in front of the gradient of the estimate of the log likelihood, ​\hat{\mathcal{F}}. This is a global signal (opposed to the local signals that are present in ​\hat{\mathcal{L}}^\mathcal{Q}) that they interpret as a novelty or surprise signal.

Reducing gradient estimation variance

The authors note that the stochastic gradient they introduced has been used extensively in reinforcement learning and that its variance is prohibitively high. To deal with this (presumably following the approach others have developed in RL, vice versa) they adopt a simple, baseline removal approach. They subtract the mean ​\bar{\mathcal{F}} of the free energy estimate ​\hat{\mathcal{F}} calculated as a moving average across several previous batches of length ​T from the current value ​\hat{\mathcal{F}}(T). They replace the free energy in the gradient for the ​\mathcal{Q} network with a free energy error signal, ​\hat{\mathcal{F}}(T) - \bar{\mathcal{F}}. Below, the log likelihood of the generated data when this procedure is used is plotted against a naively trained network, showing that this procedure works better than the naive rule.

Figure5a

Numerical results

Details of their numerical simulations:

  • Training data is binary arrays of spike data.
  • Training data comes in batches of 200 ms with 500 batches sequentially shown to the network (100 s of data).
  • During learning, visible neurons are forced to spike like the training data.
  • Log likelihood of test data was estimated with importance sampling. Given a generative model with density ​p(x_v,x_h), importance sampling allows us to estimate the density of p(x_v):

​p(x_v) = \langle p(x_v | x_h) \rangle_{p(x_h)} = \langle p(x_v | x_h) \frac{p(x_h)}{q(x_h|x_v)} \rangle_{q(x_h|x_v)}

= \langle \text{exp}[\text{log}p(x_v,x_h) - \text{log} q(x_h|x_v)] \rangle_q = \langle \text{exp}[-\hat{\mathcal{F}}(x_v,x_h)]\rangle_{q(x_v|x_h)}

Using this equation, they estimate the log likelihood of the observed spike trains by sampling several times from the ​\mathcal{Q} network and computing the average of the free energy. They use 500 samples of duration 100 from the ​\mathcal{Q} network to compute this estimate.

Here is an example of training with this method with 50 hidden units using the “stairs” dataset. C shows that the network during the “sleep phase” (running in generative mode) forms a latent representation of the stairs in the hidden layers. Running the network in “inference mode” (wake, in the wake-sleep parlance), when the ​\mathcal{Q} network synapses are being used, the model is capable of performing inference on the causes of the incoming data (the visible neurons are being driven with the data).

Figure3

Role of the novelty signal

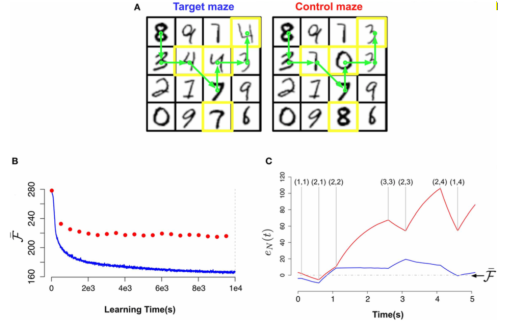
To examine the role of the novelty signal, they train a network to perform a maze task. Each maze contains 16 rooms where each room is a 28×28 pixel greyscale image of a MNIST digit. Each room is only accessible from a neighboring room. Pixel values were converted into firings rates from 0.01 to 9 Hz. In the test maze (or control maze), some of the rooms of the training maze were changed. The network had 28×28 visible units and 30 hidden units. These were recurrent binary units. Data were generated from random trajectories of 100 time steps in the target maze. Each learning epoch was 500 presentations of the data batches.

Below, (bottom left) they plotted the slow moving average of the free energy ​\bar{\mathcal{F}} as a function of the amount of observed data for the target maze (blue) and the same model when it was “teleported” to the control maze every 500 s. In the beginning of learning, the free energy is the same so the model cannot distinguish between them. As learning proceeds, the model identifies the test as unfamiliar (higher free energy).

Bottom right shows the free energy error signal for the sample trajectory in A. It fluctuates near zero for the learned maze but deviates largely for the test maze. We can see at (3,3) the free energy signal really jump up, meaning that the model identifies this as different from the target.

To conclude, the authors speculate that a neural correlate of this free energy error signal should look like an activity burst when an animal traverses unexpected situations. Also, they expect to see a substantial increase in the variance of the changes in synaptic weights when moving from a learned to a unfamiliar maze due to the change in the baseline of surprise levels.

Figure6.png

Leave a comment