Continual learning for Recurrent Neural Networks

A few weeks ago in lab meeting we discussed ‘Organizing recurrent network dynamics by task-computation to enable continual learning’ by Duncker & Driscoll et. al 2020. This paper seeks to understand how a neural population maintains the flexibility to learn new tasks while robustly executing previously learned tasks. While biological networks learn new tasks all the time in a sequential (a.k.a. continual) fashion, continual learning in artificial neural networks has proven to be hard. These networks are known to catastrophically forget previous tasks when trained on a new task. In this work, the authors come up with a learning rule that enables a recurrent neural network to learn multiple tasks sequentially without catastrophic forgetting. 

Let’s first formally define continual learning: We want to train a model on K tasks sequentially, where each task has its own set of input/output pairs represented by . Our goal is to ensure that the network performs well per some pre-decided accuracy metric on all tasks at the end of training. The key thing to keep in mind is that, unlike simultaneous training, here we train the network on one dataset at a time, such that the network does not have access to samples from previous tasks when learning a new task.

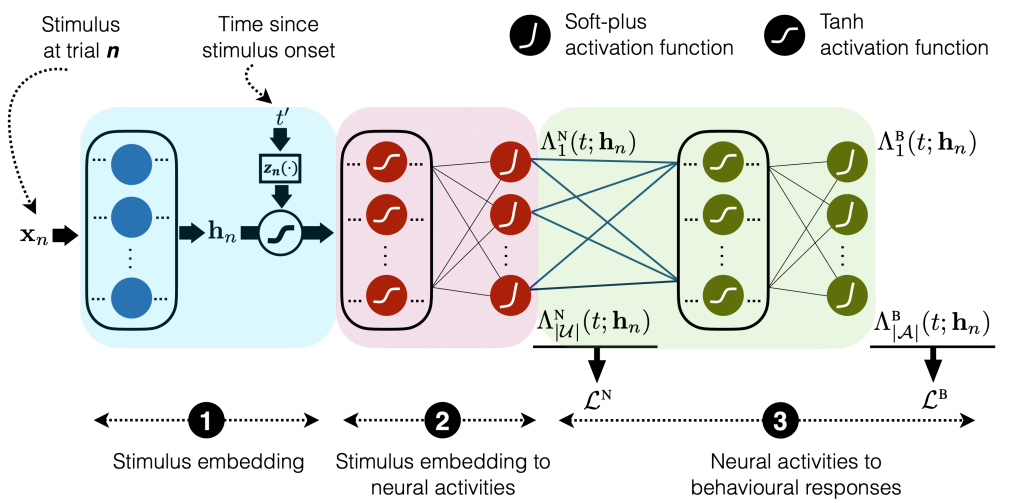
Continual learning for recurrent neural networks: This paper aims to perform continual learning using recurrent neural networks (RNNs), which are often studied as proxies for neural populations in neuroscience. The intuition behind their approach is to allow tasks that require similar computations/dynamics to use shared subspaces, while tasks that require different computations and would otherwise interfere with previously learned are encouraged to use an orthogonal subspace (see figure above).

They consider RNNs of the following form:

where is the activity of hidden states at time t, is any external input, is gaussian noise and is the output of the network. Let’s define , and focus on updating this. The same ideas also hold for . Typically, we update weights of a network as:

, where ,

and represents the loss function.

Project, and then project again: The authors modify this update rule such that:

Here, is a projection matrix that projects the weight change away from the space of all previous inputs to the network. To understand this better, let’s define the input to the hidden nodes in the network as , at time t, trial r of task k. The projection matrix ensures that for all time points within all trials of all previous tasks (this idea was introduced by Zeng et al. 2019). This preserves the network’s dynamics/outputs on any previous input, preserving its performance on all previous tasks. 

, the left hand side matrix, projects the weight updates away from the output space of the network (spanned by ). The consequence of this update rule is that , which means any changes in the weights happen orthogonal to the current weight space. Tying it back to our original intuition: when the network is trained on a new task which requires any dissimilar dynamics, they are encouraged to lie on an orthogonal subspace. However, a new task can always reuse previously learned dynamics. 

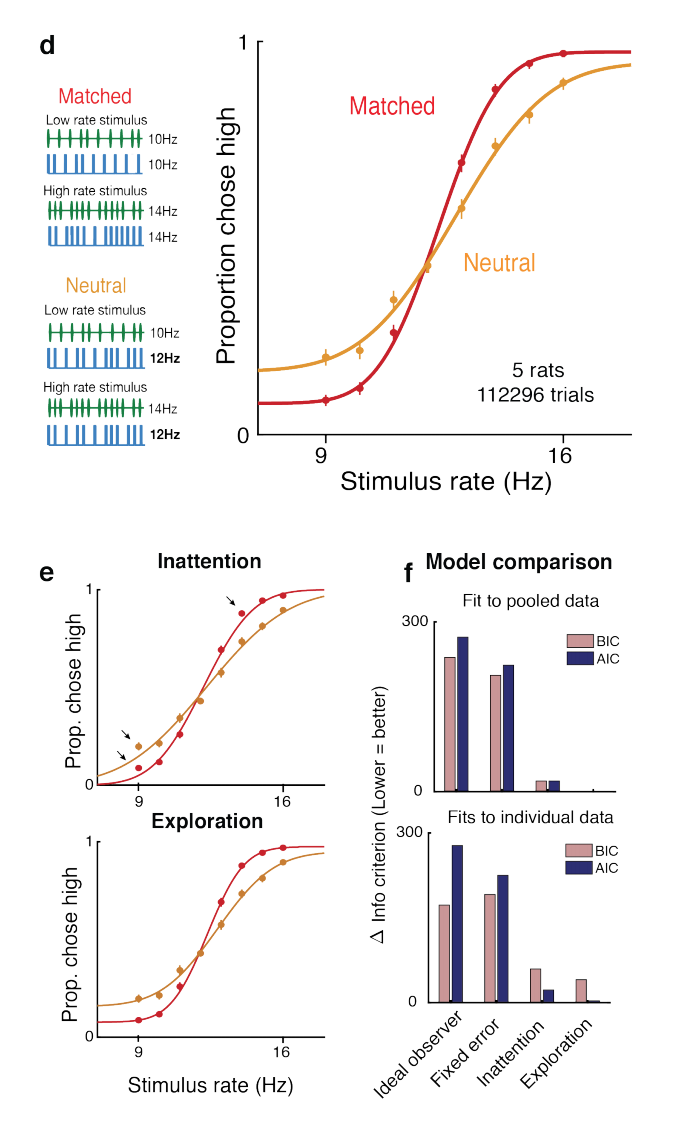
It works!  They test their method on a set of four neuroscience tasks (from Yang et al. 2019). The key results without going into task details are as follows:

1. Their approach is able to train a network sequentially on all the 4 tasks with better test performance across tasks as compared to existing methods and standard SGD (see figure; each color represents a new task).
2. They find that the underlying dynamics of hidden states of the network (near fixed points) for a task remains fixed even after the network is trained on newer tasks, showing that their training procedure is indeed robust!
3. They find empirical evidence that dynamics corresponding to some tasks evolve in shared subspaces (of the high-dimensional hidden states), while others use orthogonal subspaces. 
4. They find organizational differences between learned dynamics through sequential training and simultaneous training: simultaneous training results in slightly better results and more efficient usage of shared structure across tasks.

Questions for future research: An important question that this approach raises is whether there is an upper limit to the number of dissimilar tasks that such a learning rule can enable the network to learn. How long can we keep projecting away from the space of outputs and inputs? Furthermore, how much does the order of tasks matter as the dynamics corresponding to newer tasks can only occupy the remaining orthogonal subspace? And finally the million dollar question: how do real neurons in the brain learn new tasks sequentially?

Neural Network Poisson Models for Behavioural and Neural Spike Train Data

In this week’s lab meeting, we discussed the paper Neural Network Poisson Models for Behavioural and Neural Spike Train Data, which had been presented by Khajehnejad, Habibollahi, Nock, Arabzadeh, Dayan, and Dezfouli at ICML, 2022. This work aimed to introduce an end-to-end model that explained how the brain represents past and present sensory inputs across areas, and how these representations evolve over time and ultimately lead to behavior. While numerous supervised, reinforcement learning, and unsupervised point process-based methods do exist for examining the relationship between neural activity and behavior, these methods in general have several shortcomings including being insufficient to capture complex neural representations of inputs and actions distributed across different brain regions, not accounting for trial-to-trial variability in behavior and neural recordings, and being sensitive to the choice of bin size of spike counts.

Addressing these limitations, here the authors introduced a novel neural network Poisson process model which models a canonical visual discrimination experiment whereby, on each trial, subjects are presented with a stimulus and have to choose an option (or keep still; i.e. NoGo). The main contributions of this approach can be summarized as follows.

1. Handles variability between response times across different trials of an experiment by a temporal re-scaling mechanism:
   • For each trial , they considered spikes from unit until either a response was made at time , or to the end of time window , whichever had come first, i.e., up to . The reason for restricting the trial duration accordingly had been to model the neural processes that led to behavioral responses, rather than what happened post-response. To handle the variability of across different trials, they proposed to re-scale the original spike times using a trial-specific monotonic function , . Following this transformation, the latent neural intensity function of the inhomogeneous Poisson point process of unit at trial and time given by , where is the stimulus embedding, can be related to the corresponding canonical (trial independent) intensity function by . This facilitates the estimation of a single function to model the neuronal spiking activities across all trials while preserving details about the variability of response times across different trials. To simplify the subsequent derivations, they assumed this transformation to be linear: .
2. Flexibly learns (without any assumptions on the functional form) the connections between environmental stimuli and neural representations, and between neural representations and behavioral responses:
   • The following figure shows the model that they proposed to achieve this task, which is a neural network with three main components. The first maps the stimulus that was presented at trial through a series of fully connected layers to realize an input embedding denoted by . The second component takes the embedding and the spike times since the stimulus onset and outputs the modeled activity of each neural region at time in the form of the cumulative intensity function . The neural intensity function is then obtained by differentiating with respect to . The motivation for parameterizing the cumulative intensity functions instead of directly parameterizing the neural intensity function had been to obviate the computation of the intractable integral in the point process likelihood. The third component of the model takes the neural cumulative intensity functions and maps them to the behavioral cumulative intensity functions for making each action at each time since the stimulus onset.
3. Jointly fits both behavioral and neural data:
   • They used the neural loss function to train all the weights from stimulus to neural cumulative intensity functions (blue and red rectangles in the following figure): , where , and is the spike time relative to the stimulus onset of the spiking event of unit at trial . Given these trained neural cumulative intensity functions, then the weights connecting neural outputs to behavioral outputs (green rectangle in the following figure) had been trained using , where , and is the set of trials on which action was taken before .
4. Derives spike count statistics disentangled from chosen temporal bin sizes:
   • Since the aforementioned learning process directly uses the spike times as inputs instead of spike counts, this inference is independent of the selection of a time bin for spike count calculations.

Finally, they applied this method to two neural/behavioral datasets concerning visual discrimination tasks: one collected using Neuropixel probes (Steinmetz et al., 2019) from mice, and the other the output of a hierarchical network model with reciprocally connected sensory and integration circuits that modeled behavior in a motion-based task (Wimmer et al., 2015). They showed that this method can link behavioral data with their underlying neural processes and input stimuli in both cases and that it outperforms several existing baseline point process estimators.

Estimating the similarity between neural tuning curves.

TLDR; we suggest that an existing metric, r²_ER, should be preferred as an estimator of single neuron representational drift rather than the representational drift index (RDI, Marks and Goard, 2021) because it isn’t clear what intermediate values of RDI mean.

Often, neuroscientists quantify how similar two neural tuning curves are. The correlation coefficient is a common metric of similarity.  Yet it has a substantial downward bias proportional to how noisy the neurons are and inversely proportional to the number of repeats collected. This bias with respect to ‘measurement error’, is well known in the statistics literature but largely unaddressed in neuroscience.

The problem is made clear in the figure below, where two perfectly correlated tuning curves (solid lines, red and blue) appear to be different when noisy trial averages (red and blue circles) are used to estimate their correlation. 

Recently we (Pospisil and Bair, 2022) have developed a far more accurate estimator of tuning curve correlation. It even beats out Spearman (1904) whose approach to the problem had been the de facto standard for the past century and change.

We worked on this problem because of the ubiquity of questions pertaining to the similarity of tuning curves across neurons (w.r.t. cortical distance, image transformations, physical space, experimental conditions). Recently, though an exciting and novel area of research has begun around the similarity of tuning curves of neurons across time. It has been found that tuning curves drift and this phenomenon has been termed ‘representational drift’. 

Here we suggest that our estimator developed in the context of signal correlation could also serve as a useful metric of single neuron representational drift. Examining the literature we found a few emerging metrics of representational drift but only one among them that attempted to explicitly account for the confound of trial-to-trial variability in estimating tuning curve similarity: the representational drift index (RDI) (Marks and Goard, 2021). 

We ran a simple simulation of two neural tuning curves with noisy samples (same as the plot above) and adjusted the fraction of variance explained between them (by adjusting phase) to see how different estimators compared relative to the true r².  

We compared our metric, the naive estimator (used by a variety of authors), and RDI.  

We found that in general, the naive estimator tended to estimate two tuning curves were dissimilar when they were identical and both r²_ER and RDI accurately determined that they were identical (orange and green overlaid at 1- r² =0). On the other hand for intermediate degrees of similarity, for example when 1- r² =  0.9 RDI was only halfway to its maximal value of 1 when only 10% of tuning between the two tuning curves was shared. 

But wait a minute! Is this fair to compare RDI on the basis of r²? That is not what it was designed to estimate. 

This gets to a deeper statistical question. What is RDI supposed to be an estimator of? While qualitatively the answer seems clear ‘how similar two tuning curves are’, quantitatively it is not clear what parameter of what statistical model the metric is an estimator of. This makes RDI difficult to interpret, 

Thus we humbly suggest that r²_ER can serve as an accurate interpretable metric of representational dissimilarity. 

Estimating learnability

TL;DR: you can accurately estimate the hypothetical performance of multivariate linear regression and classification models trained on infinite data with surprisingly little data, , even when the number of samples (n) is less than the number of features or dimensions (d). 

This week in lab meeting we discussed ‘Estimating learnability in the sublinear data-regime’ by Kong and Valiant published in NeurIPS 2018. The key idea is that with clever statistical methods you can estimate the hypothetical performance of a model trained on infinite data, using only a small amount of training data. The authors provide methods to do so for multivariate linear regression and classification. 

For the multivariate regression case, the authors seek to estimate the explained variance, as quantified by:

where is the (scalar) output, is the vector () of regressors, and is the optimal least squares weight vector.

In the linear regression setting, an accurate estimator of this quantity already exists (but has a key limitation):

where is the least squares solution estimated on samples from (x, y) (same as those in the formula above). 

It’s important to note that with finite data, the estimated is not the true , thus your model wouldn’t actually achieve this performance on held-out data.

The key problem with this simple but effective estimator is that it stops working when you have fewer samples than features , this is because your regressand matrix (x) is over-complete and there is no unique least-squares solution and if you regularize you can fit the data arbitrarily well (leaving no residuals on which to estimate performance).

Kong and Valiant provide a solution to this problem by not estimating performance on the basis of model predictions but directly on the basis of covariance between your regressors and regressand. To get a flavor for this approach I will provide a short alternative derivation of their estimator in the case where Cov(x) = I, E[x]=0, E[y]=0. First note that if I choose one observation of x and y, then:

because . And with two independent observations of x and y, I can have:

.

Then, divide by an unbiased estimator of the variance of , the sample variance will work, and you have an estimate of with an unbiased numerator and denominator.

Kong and Valiant go beyond the restrictive case I describe above to arbitrary covariance and provide an excellent introduction reviewing prior work in this area (note the solution to the identity covariance case was first provided by Lee H Dicker. Variance estimation in high-dimensional linear models. Biometrika, 2014.).

New blog post on regularization by Rich Pang

To compensate for the lack of recent activity, here’s a link to a recent blog post from lab member Rich Pang, which provides a nice overview of different regularization methods, along with geometric intuition into how they work: Using regularization to handle correlated predictors

Monte Carlo gradient estimators

A couple weeks ago during lab meeting we discussed parts of Monte Carlo Gradient Estimation in Machine Learning. This is a lovely survey of the topic and unfortunately we only covered a small part of it. The things we did cover consisted the introduction, score function gradient estimators and pathwise gradient estimators. Here we will for the most part only outline a little bit of the score function estimator. Before jumping right into it let’s take a step back and consider (for this specific paper):

• The types of probabilistic objects that gradients are taken with respect to.
• Why we might want / need an estimator for the above

So what exactly are we taking gradients of? In the paper the authors introduce this object as “a general probabilistic objective” (note, for the remainder of this blog post, that all lowercase non-bold symbols except for the index variable n should be considered vector-valued quantities):

In (1) we notice that the objective involves integrating over all the possible values can become. Now if you’re at all familiar with topics in any theory/computational orientated subject you’ll recognize that integrating (1) might be rather difficult, if not impossible. With the usual culprits of having no closed form evaluation of the integral (as opposed to say for which we do have a closed form evaluation), and or issues regarding the large space of values that variables of interest can take, thus making approximation by quadrature ineffective. These reasons tell us we will need some other type of approximation. That approximation will be a Monte Carlo estimator of the expectation. Generally we can define this estimator, given samples for as (note that we are using approximately below to guide intuition, this is not the usual use of it):



One last thing that we’ll come back to later on. We note that the subject of the article and this blog post is “Monte Carlo gradient estimator”, however above I’ve outline why you might want a Monte Carlo estimator of an expectation. These two things are not necessarily the same. The gradient of the expectation is not simply the expectation of the gradient (obtained by exchanging the order of integration and differentiation), at least when the gradient is taken with respect to the parameters of the distribution itself. To make this work, we will make use of ideas from probability and statistics to write down the gradient of the expectation again as a proper expectation — thus allowing us to approximate said expectation with a Monte Carlo estimator.

So we have the thing to approximate, how we’re going to approximate it, and know what are the computational difficulties that call for an approximation to be made. What’s left is to motivate where we’d use this approximation. In short, (please refer to the original papers!) policy gradient (think reinforcement learning .i.e. Sutton & Barto), and Black Box Variational Inference both make use of what’s been outlined above (though there are other use cases!).

Both methods need to learn some set of parameters . One way to learn such parameters is through gradient descent. So we will need the gradient of the objective (which we have defined above as the expectation), which is (as usual):



This now calls us to refine our words a bit. We’re not trying to arrive at a Monte Carlo estimator of the expectation per-se, rather we want a Monte Carlo estimator of the gradient of that expectation. This is where the score function estimator and the pathwise estimator come into play. The score function is defined as the gradient of the log of the function . Thus it is (by the chain rule of differentiation):



This is useful because it is an expression relating the gradient of the function of interest to the gradient of its log. That’s good to know but why is it useful for what we hope to accomplish? This becomes clearer if we write out the gradient of the expectation (under conditions that allow the interchange of integration and differentiation):



note now that the goal is to arrive at a Monte Carlo estimator of the expectation, however in (4) the right most side of you’ll note that we no longer have an expectation. This is because has become , and the gradient does not in general satisfy the conditions to be considered a proper probability (e.g. the gradient can be negative!). However, due to the expression given by the definition of the score function, we can replace by . Plugging this back in the the right most side of (4) we have:



which brings us back into the realm of computing a proper expectation and we can now use (2) to write down the form of the estimator:



Now for the pathwise estimator. In the score function estimator we took the gradient of , for the pathwise estimator we will take the gradient of . The general reasoning behind why we’d want to do it, why it helps us achieve our goal is exactly the same as stated above. That is, when we take the gradient of the regular definition of the expectation, we no longer have an expectation. However for the reason of why’d you want to use the pathwise estimator over the score function we refer you to the original article. The name “pathwise” is motivated by two equivalent ways to sample a random variant from . The first we are familiar with: , and have used in the score function. The second and equivalent way to do this is by sampling a random variant from a simpler, continuous distribution: , and then transforming that variant via some function , that “encodes” the distributional parameters of the “end” distribution of interest. For a concrete example of what this means (which the authors give in the paper), say . The “path” version of sampling a random variant , is by first sampling . Then we define the function : . So we have that , where , and the random variant is now . The form of this estimator is then:



Unfortunately that’s all we’ll get into for now. Please do take a look at the original article. Thanks for checking out the lab blog and happy holidays!

Tutorial on Normalizing Flows

Today in lab meeting, we continued our discussion of deep unsupervised learning with a tutorial on Normalizing Flows. Similar to VAEs, which we have discussed previously, flow-based models are used to learn a generative distribution, , when this is arbitrarily complex and may, for example, represent a distribution over all natural images. Alternatively, in the context of neuroscience, may represent a distribution over all possible neural population activity vectors. Learning can be useful for missing data imputation, dataset augmentation (deepfakes) or to characterize the data generating process (amongst many other applications).

Flow-based models allow us to efficiently and exactly sample from , as well as to efficiently and exactly evaluate . The workhorse for Normalizing Flows is the Change of Variables formula, which maps a probability distribution over to a simpler probability distribution, such as a multivariate Gaussian distribution, over latent variable space . Assuming a bijective mapping , the Change of Variables formula is

where is the absolute value of the determinant of the Jacobian. This term is necessary so as to ensure probability mass is preserved during the transformation. In order to sample from , a sample from can be converted into a sample from using the inverse transformation:

Flow-models such as NICE, RealNVP, and Glow utilize specific choices for so as to ensure that is both invertible and differentiable (so that both sampling from and evaluating are possible), and so that the calculation of is computationally tractable (and not an operation, where is the dimension of ). In lab meeting, we discussed the Coupling Layers transformation used in the RealNVP model of Dinh et al. (2017):

This is an invertible, differentiable mapping from latent variables , which are sampled from a multivariate normal distribution, to the target distribution. Here ‘‘ denotes elementwise multiplication and and are functions implemented by neural networks. The RealNVP transformation results in a triangular Jacobian with a determinant that can be efficiently evaluated as the product of the terms on the diagonal. We examined the JAX implementation of the RealNVP model provided by Eric Jang in his ICML 2019 tutorial.

As a neural computation lab, we also discussed the potential usefulness of flow-based models in a neuroscience context. Some potential limitations to their usefulness may lie in the fact that they are typically used to model continuous probability distributions; yet in neuroscience, we are often interested in Poisson-like spike distributions. However, recent work on dequantization, which describes how to model discrete pixel intensities with flows, may provide inspiration for how to handle the discreteness of neural data. One other potential limitation to their usefulness related to the fact that the dimensionality of the latent variable in flow-models is equal to that of the observed data. In neuroscience, we are often interested in finding lower-dimensional structure within neural population data; so flow-based models may not be well-suited for this purpose. Regardless of these potential limitations; it is clear that normalizing flows models are powerful and we look forward to continuing to explore their applications in the future.

Step-by-step procedure for choosing a learning rate (and other optimization hyperparameters)

I’ve been using deep neural networks (DNNs) in my research. DNNs, as is often preached, are powerful models, capable of mapping almost any function. However, after the sermon is over, someone starting to train a DNN in the wild can quickly be overwhelmed by the many subtle technical details involved. The architecture, regularization techniques, and optimization are all inter-related, and these relationships change for different datasets.

My first steps in training a DNN primarily focused on architecture—do I have enough layers and filters for my problem? The optimization—stochastic gradient descent (SGD) with all of its hyperparameters (learning rate, momentum, …) and variants—was an afterthought, and I chose hyperparameters that seemed reasonable. Still, a nagging question persisted in the back of my mind: What if different hyperparameters led to even better performance? It was an obvious case of fear-of-missing-out (FOMO).

Grid search (aka brute force) and black-box optimization techniques should be last resorts.

Due to FOMO, I began to more properly choose my hyperparameters by using a grid search (e.g., random search). This takes a lot of time. For each tweak of the architecture, I would need to rerun the entire grid search. For each grid search, out popped a solution and nothing else—no intuition about my problem, no understanding about the tradeoffs of the hyperparameters, and no clear way to check my code for bugs (except evaluating performance). The same can be said for black-box optimization techniques—which are fancier versions of grid search. I felt ashamed each grid search I ran because it’s brainless. It encourages me not to think about my data, model, or the bridge between the two: optimization.

Let’s use our intuition about optimization to help guide our choice of hyperparameters.

Optimization is not a black-box method. In fact, gradient descent is one of the most intuitive concepts in math: You are a hiker on top of a mountain, and you need to get down. What direction and how far do you move? Inspired by this, I started reading about other ways to choose optimization hyperparameters. I came up with a step-by-step procedure that I now follow for every problem. It’s largely inspired by Smith 2018 and Jordan 2018.

This procedure outputs:
1) reasonable values for the hyperparameters,
2) intuition about the problem, and
3) red flags if there are bugs in your code.
The procedure takes a couple of training runs (fast!).

[Note: This procedure is great for researchers who want to get a model up and running. Grid/black-box search is more appropriate for architecture searches and when you really care about gaining 1% in accuracy.]

Step-by-step procedure:

Here’s the full procedure. I’ll discuss each step individually.

1. Compute initial line search.
2. Increase learning rate.
3. Increase momentum.
4. Check if learning rate decay helps.
5. Check if a cyclical learning rate helps.
6. (optional) Check your other favorite SGD variants.
7. Compute final line search, for closure.

The procedure is general for any architecture and problem. For an example problem, I run the procedure on a small (3-layer) convolutional neural network to predict the responses of visual cortical neurons from image features (see Cowley and Pillow, 2020). I report accuracy on heldout data, as we want to make sure our optimized solution generalizes. The description of each step is short for ease of mind; I assume you are familiar with optimization and SGD (if you aren’t, check out the Convex Optimization book).

For a quick review, here is the equation for gradient descent:

And here are the equations for gradient descent with momentum:

Step 1: Compute initial line search.

• Choose a direction in weight space (found either by training on a small amount of data or choosing weights randomly). 
• Perform a line search by taking small steps (linear increments) along that direction, plotting accuracy for each step.

• How nonconvex/complicated is your accuracy landscape? Here, I have a nonconvex problem with a meandering slope and a sharp ridge with a cliff.
  → Choosing a large learning rate may mean I fall off the cliff!

Step 2: Increase learning rate.

• Start with an epsilon-small learning rate. Then, increase the learning rate for each consecutive training epoch.

• Small learning rates lead to small increases in accuracy.
  → You’ve barely moved in weight space.
• Large learning rates lead to large decreases in accuracy.
  → You’re moving too far, and you’ve jumped off the cliff!
• Just right learning rates are where the accuracy increases steadily.
• Here, we choose a learning rate of 1.5.

Step 3: Increase momentum.

• Train for N epochs with the chosen learning rate.
• Similar to Step 2, start with a small momentum and increase it each training epoch.

• A small momentum yields only a small increase in accuracy.
  A large momentum sees a drop in accuracy. 
• Choose a momentum in the sweet spot—where accuracy is steadily increasing.
• Here, we choose a momentum of 0.7.

• Using the chosen learning rate and momentum, train for N epochs. Confirm that momentum improves performance.

• Thoughts: Momentum does help in this case (red above black).

Step 4: Check if learning rate decay helps.

• Train model until convergence (might be longer than N epochs). 
• Use a schedule for learning rate decay. The idea is that as you get closer to an optimum, you should make smaller steps (i.e., decay) to prevent yourself from jumping passed the optimum. Lots of choices here.
• My schedule is a power decay:
  Let M be the epoch number where performance plateaus/falls off.
  Then alpha = (⅔)^(1/M).
  

• Train model with learning rate decay. Confirm learning rate decay is needed.

• Thoughts: Learning rate decay is not really helpful for my problem. So I won’t use it.

Step 5: Check if a cyclical learning rate helps.

• Use a cyclical learning rate. The idea is that you may want to explore different optima, so we need a way to push ourselves far from the current optimum. 
  
  Here’s one option:
  • Choose the upper learning rate bound as 2 * chosen learning rate.
  • Choose the lower learning rate bound as ½ * chosen learning rate.
  • Start the learning rate at the upper bound then shrink to the lower bound after M epochs (where M is chosen from Step 4). Then, switch back to the largest learning rate:

• Train model with a cyclical learning rate. Confirm that a cyclical learning rate is needed.

• Thoughts: A cyclical learning rate does train faster, but not substantially. So I won’t use it.

Step 6: (optional) Check your other favorite SGD variants.

• Likely everyone has their favorite SGD variant. Try it here!
  Note: Don’t use the hyperparameters chosen above for some SGD variants, like Adam (which usually assumes a very small initial learning rate). Instead, you may need to repeat some steps to find the variant’s hyperparameters.
• I ran Adam on the same dataset, choosing a learning rate of 1-e2 (much smaller than the learning rate of 1.5 chosen in Step 1!).

• Adam does well in the beginning, likely because it adapts its learning rate and can get away with a large learning rate for the earlier epochs.
• I’ve found that Adam doesn’t always work well. This is especially true when training a DNN to predict behavior of different subjects—each subject’s behavior (e.g., velocity) may have a different variance. This is why we check!

Step 7: Compute final line search, for closure.

• This is my favorite step. It’s the exact same as Step 1, except we now compute a line search in weight space along a line between the initial, untrained weight vector and the final, trained weight vector.

• Thoughts: This looks very similar to Step 1. The optimization first finds the ridge and then moves along this ridge.
• In this example, there doesn’t seem to be multiple local minima. But this is not always the case!  Here’s a final line search from one of my other research projects:

Final thoughts

You can see why I like this procedure so much. It takes about an afternoon to run, and I get some interesting plots to look at and think about. The procedure outputs a nice set of hyperparameters, some intuition about the optimization problem we face, and gives me peace of mind that I shouldn’t keep twiddling hyperparameters and preventing my FOMO.

It would be great to have a gallery of observed final line searches (Step 7), just to see the variety of loss landscapes out there. In the meantime, you can check out these artistic renderings of loss landscapes: losslandscape.com. 

Attention is all you need. (aka the Transformer network)

No matter how we frame it, in the end, studying the brain is equivalent to trying to predict one sequence from another sequence. We want to predict complicated movements from neural activity. We want to predict neural activity from time-varying stimuli. We even want to predict neural activity in one brain area from neural activity in another area. Thus, as computational neuroscientists, we should be intimately familiar with new machine learning techniques that allow us to better relate one sequence to another.

One sequence-to-sequence problem receiving a lot of interest in machine learning is “translation”—converting a sentence in one language (e.g., English) to another (e.g., Polish). The main challenge is getting context correct. For example, consider “bark” for the following sentences: “The bark is loud.” and “The bark is brown.” In Polish, bark would be “szczekanie” and “kora,” respectively, based on context. Machine learning folks have devised some ingenious architectures to tackle this problem. In this post, I’ll talk about one architecture that is unexpected but seems to work quite well: Transformer networks. This architecture was proposed in “Attention is all you need.” by Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, Polosukhin, NIPS 2017.

High-level intuition

The Transformer network relies on an encoding-decoding approach. The idea is to “encode” the input sequence into a latent representation (i.e., an embedding) that is easier to work with. This embedding (typically a vector of abstract variables) is then “decoded” into an output sequence (e.g., another language). Our problem, then, is to design a “useful” embedding for translation, and build an architecture that can express it.

What properties do we want our embedding to have? One property is a measure of similarity— “tomato” is more similar to “blueberry” than to “chair.” An embedding with this property has been solved with word2vec. Another important property is context—is “tomato” the subject? direct object? is it modified by “tasty” or “rotten”? It turns out we can incorporate context by adding embeddings together. For example, let embeddings e1=”tomato” and e2=”tasty”. Then
e3 = e1 + e2 corresponds to an embedding of a “tasty tomato”. We can keep tacking on more context (e.g., e4 = “subject of sentence”, e5 = “the”, e6 = “belongs to Tom”, etc.). With this embedding property, if we come across an ambiguous word like “it”, we simply find the word that “it” refers to, and add that word to the embedding!

Architecture: Stacked attention layers

The authors came up with a way to efficiently search for context and add that context to the embedding. They use “attention”—in the general sense of the word, not based on neuroscience—as a way to find distant relationships between words. Figure 1 is a stylized version of this computation. The idea is, given a word, compare this word with all other words in the sentence for a specific context. For example, if the word is “sees”, attention will try to find “who sees?” and “sees what?” If attention finds answers to its context questions, these answers will be incorporated into the embedding via a linear combination. If attention does not receive answers, no harm is done—attention will simply pass on the unmodified word embedding (i.e., weights for the other words will be zero).

Figure 1: The attention mechanism. (this is my first time making gifs—sorry for the blurriness!)

One can imagine that having one level of attention may not be the best way to extract the structure of natural language. Just like we learned in sixth grade, sentences have hierarchical structure (did you also have to draw those syntax trees?). So, we should stack levels of attention. The lower levels correspond to easy questions (“Is there an adjective to this noun?”) that likely involve only two or three words of the input sequence. The deeper levels correspond to more nuanced questions (“What is the direct object of this sentence?”) that span most if not all of the input sequence. To achieve this, the authors stacked layers of attention on top of each other. To decode, they basically reverse the process. Figure 2 is an illustration of this process. 

Figure 2: Attention blocks form an encoder stack, which feeds into a decoder stack.

The authors claim this approach minimizes the distance of relating one position in a sequence to another. This is because attention looks at all pairwise interactions, while other architectures (such as recurrent neural networks) sequentially look at the input sequence (making it difficult to compare the first word to the last word). The primary point of confusion while reading the paper was how input sequences were fed into the network (hopefully Fig. 2 clarifies this—each word embedding is transformed in parallel to other word embeddings. If you input N words, each encoder will output N embeddings). This architecture produced state-of-the-art results, and has since been used in many different natural language processing tasks. It also uses many bells and whistles (residual blocks, layer normalization, …)—it will be interesting to see future work argue which components are the most important for this architecture.

Getting back to the neuroscience

As computational neuroscientists, we should take advantage of these architectures (which have been designed and trained with the aid of GPU armies), and use them to help solve our own problems. One aspect of this work (and in natural language processing in general) is the idea of adding two embedding vectors to form a more “context-relevant” embedding. This is missing from our current latent variable models. More importantly, it may be a way in which the brain also encodes context. I also think this type of attention computation will be useful when we are trying to predict sequences of natural behavior, where we cannot make use of task structure (e.g., a delay period, stimulus onset, etc.). Experimentalists are now collecting massive datasets of natural behavior—a perfect opportunity to see how this attention computation holds up!

Sutton & Barto Mini-Bootcamp

This week in lab meeting, I presented a mini-bootcamp covering Richard Sutton & Andrew Barto’s Reinforcement Learning, Part 1: Tabular Solution Methods (Chapters 2-8). My attempt to get through 170 pages of material in 75 minutes can be found below (as .pptx or .pdf):

suttonbartopt1_pillowlab_062719.pptx

suttonbartopt1_pillowlab_062719.pdf

Lapses in perceptual judgments reflect exploration

In lab meeting this week, we discussed Lapses in perceptual judgments reflect exploration by Pisupati*, Chartarifsky-Lynn*, Khanal and Churchland. This paper proposes that, rather than corresponding to inattention (Wichmann and Hill, 2001), motor error, or -greedy exploration as has previously been suggested, lapses (errors on “easy” trials with strong sensory evidence) correspond to uncertainty-guided exploration. In particular, the authors compare empirically-obtained psychometric curves characterizing the performance of rats on a 2AFC task, with predicted psychometric curves from various normative models of lapses. They found that their softmax exploration model explains the empirical data best.

Empirical psychometric curve

Psychometric curves are used to characterize the behavior of animals as a function of the stimulus intensity when performing, for example, 2AFC tasks. They are defined by four parameters:

where is a sigmoidal curve (we will assume the cumulative normal distribution in what follows); determines the decision boundary and is the inverse slope parameter. is the lower asymptote of the curve, while is the upper asymptote. Together, , comprise the asymmetric lapse rates for the “easiest” stimuli (highest intensity stimuli).

While Bayesian ideal observer models have been able to motivate the cumulative normal shape of the psychometric curve (as the authors show in their Methods section), this paper aims to compare different normative models to explain the and parameters of the psychometric curve.

Inattention model

For their inattention model, the authors assume that, with probability , the rat pays attention to the task-relevant stimulus, while, with probability , it ignores the stimulus and instead chooses according to its bias . That is:

or, equivalently, and .

Softmax exploration model

In comparison to the inattention model, which assumes that, when the animal is paying attention to the task-relevant variable, it chooses the action corresponding to the maximum expected action-value, ; the softmax-exploration model assumes that the animal chooses to go right in a 2AFC task according to

where is the inverse temperature parameter and controls the balance between exploration and exploitation and is the difference in the expected value of choosing Right compared to choosing Left (see below). In the limit of , the animal will once again choose its action according to ; while in the low regime, the animal is more exploratory and may choose actions despite them not having the largest expected action values.

In the task they consider, where an animal has to determine if the frequency of an auditory and/or visual cue exceeds a predetermined threshold, the expected action values are , where is the posterior distribution over the category of the stimulus (whether the frequency of the generated auditory and/or visual stimuli are above or below the predetermined threshold) given the animal’s noisy observations of the auditory and visual stimuli, and . is the reward the animal will obtain if it chooses to go Right and is correct. Similarly, .

The authors show that the softmax exploration model corresponds to setting the lapse parameters as

and

Model Comparison

The authors compare the empirically obtained psychometric curves with those predicted by the inattention and exploration models for two experimental paradigms:

1. Matched vs Neutral Multisensory stimuli: in this experiment, rats are either presented with auditory and visual stimuli of the same frequency (‘matched’), or with auditory and visual stimuli, where one of the channels has a frequency close to the category threshold, so is, in effect, informationless (‘neutral’). The idea here is that both matched and neutral stimuli have the same ‘bottom-up salience’, so that the parameter is the same for both matched and neutral experiments in the inattention model. By contrast, there is no such restriction for the softmax exploration model, and there is a different exploration parameter for the matched and neutral experiments. The authors find that the psychometric curves corresponding to the softmax model resemble the shape of the empirically obtained curves more closely; and that BIC/AIC are lower for this model.
2. Reward manipulations: whereas the reward for choosing left or right was previously equal, now the reward for choosing right (when the frequency is above the predetermined threshold) is either increased or decreased. Again, the authors find that the psychometric curves corresponding to the softmax model resemble the shape of the empirically obtained curves more closely; and that BIC/AIC are lower for this model.

(Part of) Figure 3 of Pisupati*, Chartarifsky-Lynn*, Khanal and Churchland. The authors compare the shape of the empirically obtained psychometric curves for the matched and neutral experiments with those obtained by constraining the parameter to be the same for both matched and neutral conditions for the inattention model. In contrast, the parameter is allowed to differ for matched and neutral conditions for the exploration model. The resulting psychometric curves for the exploration model more closely resemble those in (d) and also fit the data better according to BIC/AIC.

(Part of) Figure 4 of Pisupati*, Chartarifsky-Lynn*, Khanal and Churchland. Top: The inattention, exploration and fixed error models (the latter of which we did not discuss), make different predictions for the shape of the psychometric curve when the size of the reward on the left and right is modified from equality. Bottom: the empirically determined psychometric curves. Clearly, the empirically determined psychometric curves resemble the curves from the exploration model more closely.

Reflections on this paper

By demonstrating that lapse rates can be manipulated with rewards or by using unisensory compared to multisensory stimuli, this paper highlights that traditional explanations for lapses as being due to a fixed probability of the animal neglecting the task-relevant stimulus; motor-error or greedy exploration are overly-simplistic. The asymmetric effect on left and right lapse rates of modified reward is particularly interesting, as many traditional models of lapses fail to capture this effect. Another contribution that this paper makes is in implicating the posterior striatum and secondary motor cortex as areas which may be involved in determining lapse rates; and better characterizing the role of these areas in lapse behavior than has been done in previous experiments.

This being said, some lab members raised some questions and/or points of concern as we discussed the paper. Some of these points include:

1. We would have liked to see further justification for keeping the same across the matched and neutral experiments and we question if this is a fair test for the inattention model of lapses. Previous work such as Körding et al. (2007) makes us question whether the animal uses different strategies to solve the task for the matched and neutral experiments. In particular, in the matched experiment, the animal may infer that the auditory and visual stimuli are causally related; whereas in the neutral experiment, the animal may detect the two stimuli as being unrelated. If this is true, then it seems strange to assume that and for the inattention model should be the same for the matched and neutral experiments.
2. When there are equal rewards for left and right stimuli, is there only a single free parameter determining the lapse rates in the exploration model (namely )? If so, how do the authors allow for asymmetric left and right lapse rates for the exploration model curves of Figure 3e (that is, the upper and lower asymptotes look different for both the matched and neutral curves despite equal left and right reward, yet the exploration model seems able to handle this – how does the model do this?).
3. How could uncertainty be calculated by the rat? Can the empirically determined values of be predicted from, for example, the number of times that the animal has seen the stimulus in the past? And what were some typical values for the parameter when the exploration model was fit with data? How exploratory were the rats for the different experimental paradigms considered in this paper?

The Lottery Ticket Hypothesis

Deep learning is black magic. For some reason, a neural network with millions of parameters is not cursed to overfit. Somewhere, either in the architecture or the training or the weights themselves, exists a magic that allows deep neural networks to generalize.  We are now only beginning to understand why this is.  As in most cases in science, a good starting place is to observe a paradox about the system, suggest a hypothesis to explain the paradox, and then test, test, test.

The Paradox: This week we discussed “The lottery ticket hypothesis: Finding sparse, trainable neural networks” by Frankle and Carbin, ICML, 2019. Recent studies have shown that a deep neural network can be pruned down to as little as 10% of the size of the original network with no loss in test prediction. This leads to a paradox: Training the small, pruned network (randomly initialized) leads to worse test prediction than training a large network and then pruning it. This is heresy to the ML doctrine of “Thou shalt start simple, and then go complex.” What is going on?

The Hypothesis: This paradox suggests that the initialization of the weights of the pruned network matters.  This leads to the Lottery Ticket Hypothesis:

The Lottery Ticket Hypothesis: “dense, randomly-initialized, feed-forward networks contain subnetworks (i.e., winning tickets) that—when trained in isolation—reach test prediction comparable to the original network in a similar number of iterations.” 

These “winning tickets” start out with an initialization that make training particularly effective.  If the winning tickets were re-initialized randomly, they would no longer be winning tickets—training would not reach the same level of test prediction. This may explain why deep and wide networks tend to perform better than shallow, narrow networks—> the deeper, wider networks have more chances of having the winning ticket. It also suggests that training a neural network is akin to stochastic gradient descent seeking out these winning tickets.

The Test, Test, Test: To find the winning ticket, the authors employ iterative pruning. They start with a large neural network, train it a bit, set the smallest-magnitude weights to zero (these weights are no longer trainable), rewind the trainable parameters to their original initialized values, and train again. This is repeated until pruning drastically hurts test prediction. They find that these winning tickets can be as sparse as 3.7% of the original network’s size while having the same if not higher test prediction (Figure 1, solid lines). Interestingly, if they randomly re-initialize the weights of these pruned networks, test prediction decreases considerably  (Figure 1, dashed lines, ‘reinit’). Thus, we have a way to identify winning tickets, these winning tickets are a measly fraction of the size of the original network, and their original initialization is crucial to train them.  The authors do a thorough job of confirming the robustness of this effect (45 figures in all). However, they did not investigate the properties of the subnetworks (e.g., did pruning happen most in the deeper layers?).

Figure 1. Winning tickets (subnetworks of large, original network) still maintain high test prediction (solid lines; 7.1% has higher accuracy than 100%). If these winning tickets were randomly initialized then trained (reinit), test prediction suffers (dashed lines below solid lines at 7.1%). Results include three convolutional neural networks at different depths trained and tested on the CIFAR10 image dataset. Figure reproduced from Frankle and Carbin, 2019.

One question I had remaining is if these winning tickets were necessary or sufficient to train the large network.  One analysis that could get at this question is the following. First, identify a winning ticket, and then re-initialize its weights in the original, large network. This ensures that this subnetwork is no longer is a winning ticket. Keep repeating this process.  After removing winning tickets, does the large network fail to train? How many winning tickets does the large network have?  Will the large network always have a winning ticket?  We could also do the reverse of this: For a large network, keep initializing subnetworks that are winning tickets.  Is it the case that with more winning tickets, the network trains faster with higher test prediction?

Implications for deep learning: There are several implications for deep learning. 1. Finding out what is special about the initializations of these winning tickets may help us improve initialization strategies. 2. We may be able to improve optimization techniques by better guiding stochastic gradient descent to find and train the winning ticket as fast as possible. 3. New theory that focuses on subnetworks may lead to more insight into deep learning.  4. These winning tickets may be helpful for solving other tasks (i.e., transfer learning). There have already been some follow up studies about these issues and re-examining the lottery ticket hypothesis:  Liu et al., 2019, Crowley et al., 2019, Frankle et al., 2019, Zhou et al, 2019.

Does the brain have winning tickets? I had one recurring thought while reading this paper: I know brains prune synaptic connections substantially during development—could the brain also consist of whittled-down winning tickets? After some searching, I realized that it is largely unknown the amount of pruning that occurs or when certain pruning happens.  What would be some tell-tale signs of winning tickets?  First, substantial pruning should occur (and likely does…perhaps as much as 50%). Second, randomly initializing a developing circuit should lead to a drop in performance after the same amount of training as a control subject (not sure if we can randomly set synaptic weights yet). Third, what would happen if we could prune small-magnitude synaptic connections ourselves during development? Could the brain recover? These tests could first be carried out in insects, where we have gene lines, optogenetics, whole-brain recordings, and well-labeled cell types. 

Deep Neural Networks as Gaussian Processes

In lab meeting this week, we read Deep Neural Networks as Gaussian Processes by Lee, Bahri, Novak, Schoenholz, Pennington and Sohl-Dickstein, and which appeared at ICLR 2018. The paper extends a result derived by Neal (1994); and the authors show that there is a correspondence between deep neural networks and Gaussian processes. After coming up with an efficient method to evaluate the associated kernel, the authors compared the performance of their Gaussian process model with finite width neural networks (trained with SGD) on an image classification task (MNIST, CIFAR-10). They found that the performance of the finite width networks approached that of the Gaussian process performance as the width increased, and that the uncertainty captured by the Gaussian process correlated with mean squared prediction error. Overall, this paper hints at new connections between Gaussian processes and neural networks; and it remains to be seen whether future work can harness this connection in order to extend Gaussian process inference to larger datasets, or to endow neural networks with the ability to capture uncertainty. We look forward to following progress in this field.

Single Layer Neural Networks as Gaussian Processes – Neal 1994

Let us consider a neural network with a single hidden layer. We can write the ith output of the network, , as

where is the post-activation of the jth neuron in the hidden layer; is some nonlinearity, and is the kth input to the network.

If we now assume that the weights for each layer in the network are sampled i.i.d. from a Gaussian distribution: , ; and that the biases are similarly sampled: and ; then it is possible to show that, in the limit of , , for a kernel which depends on the nonlinearity. In particular, this follows from application of the Central Limit Theorem: for a fixed input to the network , as where (which is the same for all ).

We can now apply a similar argument to the above in order to examine the distribution of ith output of the network for a collection of inputs: that is we can examine the joint distribution of . Application of the Multidimensional Central Limit Theorem tells us that, in the limit of ,

,

where and and .

Since we get a joint distribution of this form for any finite collection of inputs to the network, we can write that , as this is the very definition of a Gaussian process.

This result was shown in Neal (1994); and the precise form of the kernel was derived for the error function (a form of sigmoidal activation function) and Gaussian nonlinearities in Williams (1997).

Deep Neural Networks as Gaussian Processes

Lee et al. use similar arguments to those presented in Neal (1994) to show that the th output of the th layer of a network with a Gaussian prior over all of the weights and biases is a sample from a Gaussian process in the limit of . They use an inductive argument of the form: suppose that (the jth output of the th layer of the network is sampled from a Gaussian process). Then:

is Gaussian distributed as and any finite collection of will have a joint multivariate Gaussian distribution, i.e., where

.

If we assume a base kernel of the form , these recurrence relations can be solved in analytic form for the ReLU nonlinearity (as was demonstrated in Cho and Saul (2009)), and they can be solved numerically for other nonlinearities (and Lee et al., give a method for finding the numerical solution efficiently).

Comparison: Gaussian Processes and Finite Width Neural Networks

Lee et al. went on to compare predictions made via Gaussian process regression with the kernels obtained by solving the above recurrence relations (for nonlinearities ReLU and tanh), with the predictions obtained from finite width neural networks trained with SGD. The task was classification (reformulated as a regression problem) of MNIST digits and CIFAR-10 images. Overall, they found that their “NNGP” often outperformed finite width neural networks with the same number of layers for this task; and they also found that the performance of the finite width networks often approached that of the NNGP as the width of these networks was increased:

Figure 1 of Lee et al. The authors compare the performance of their NNGP to finite width neural networks of the same depth and find that, for many tasks, the NNGP outperforms the finite width networks and that the performance of the finite width networks approaches that of the NNGP as the width is increased.

oi-VAE: output interpretable VAEs

We recently read oi-VAE: Output Interpretable VAEs for Nonlinear Group Factor Analysis, which was published at ICML in 2018 by Samuel Ainsworth, Nicholas Foti, Adrian Lee, and Emily Fox. This paper proposes a nonlinear group factor analysis model that is an adaptation of VAEs to data with groups of observations. The goal is to identify nonlinear relationships between groups and to learn latent dimensions that control nonlinear interactions between groups. This encourages disentangled latent representations among sets of functional groups. A prominent example in the paper is motion capture data, where we desire a generative model of human walking and train on groups of observed recorded joint angles. 

Let us consider observations that we group into groups .  We note that the paper does not discuss how to choose the groups and assumes that a grouping has already been specified. The generative model maps a set of latent variables to group-specific generator networks via group-specific mapping matrices   such that

for each .

oi-VAE generative model (Ainsworth et al., 2018)

For learning interpretable sets of latents that control separate groups, the key feature of this approach is to place a sparsity-inducing prior on the columns of each . The authors use a hierarchical Bayesian sparse prior that when analytically marginalized corresponds to optimizing a group lasso penalty on the columns of .

The model is trained in the standard VAE approach by optimizing the ELBO with an amortized inference network , with the addition of the group lasso penalty and a prior on the parameters of the generator networks

where is the -th column of and is a parameter controlling the sparsity. The prior fixes the scaling of the neural network parameters relative to the mapping matrices .

The above objective consists of a differentiable term (the ELBO plus log prior on ) plus a convex but non-differential term (group LASSO). Therefore the authors use proximal gradient methods to optimize it. First, they update all parameters using the gradients of the ELBO plus log-prior with respect to , and . Then, they apply the proximal operator

to each to respect the group lasso penalty, where is a step-size. The authors fixed for all of their experiments fitting oi-VAE, so one question I had reading was how the authors determined and how varying affects the results.

The authors validate the approach on a toy example. They generated synthetic bars data, where one row of a square matrix was sampled from a Gaussian with non-zero mean while the rest of the matrix was sampled from zero-mean noise. The authors fit oi-VAE with each group set to a row of observations, and found that the model learned the appropriate sparse mapping where each latent component mapped to one of the rows. This latent space improved on the VAE, which did not have any discernible structure in the latent space. Importantly, oi-VAE still successfully identified the correct number of latent components (8) and sparse mapping even when the model was fit with double the amount of components.

 

(a) Synthetic bar data example and (b) reconstruction from oi-VAE. The learned oi-VAE latent-group mappings (c) match the true structure, while a VAE (d) does not learn a sparse structure. 

 

After validating the approach, the authors applied it to motion capture data. Here, the output groups were different joint angles. They trained the oi-VAE model on walking motion capture data. The learned latent dimensions nicely corresponded to intuitive groups of joint angles, such as the left leg (left foot, left lower leg, left upper leg). Next, the imposed structure in the model helped it generate more realistic unconditional samples of walking than the VAE, presumably because the inductive bias allowed oi-VAE to better learn invalid joint angles.

Unconditional walking pose samples from the VAE and oi-VAE models.

These results suggest the oi-VAE is a useful model for discovering nonlinear interactions between groups. In particular, I liked the approach of adding structure in the generative model to gain interpretability, and hypothesize that adding other forms of structure to VAE generative models is a good way to encourage disentangled representations (see a recent example of this in Dieng et al., 2019).

Two questions when using the approach are how to choose and how to choose the grouping of the data, as this work assumes a grouping has been chosen. In some data we may have prior knowledge about a natural grouping structure but that will not always be the case. However, even without multiple groups, the approach could be useful for learning the number of latent dimensions useful for explaining the amount of data. Finally, we point the reader to factVAE, where the authors further develop this idea to simultaneous learn complementary sparse structure in the inference network and generative model.

Uncertainty Autoencoders: Learning Compressed Representations via Variational Information Maximization

This week we continued the deep generative model theme and discussed Uncertainty Autoencoders: Learning Compressed Representations via Variational Information Maximization. This work is in the context of statistical compressive sensing, which attempts to recover a high-dimensional signal from low dimensional measurements in a way that leverages a set of training data . This is in contrast to traditional compressive sensing, which a priori asserts a sparsity based prior over and learns the recovery of a single from a single compressed measurement .

The central compressive sensing problem can be written as

.

In traditional compressive sensing,  is a known random Gaussian matrix that takes linear combinations of the sparse signal to encode . Here, describes additive Gaussian noise. The goal of compressive sensing is to decode , given measurements . This is traditionally done via LASSO, which minimizes the convex optimization problem . In contrast, statistical compressive sensing is a set of methods which recovers from using a procedure that results from training on many examples of . That is, the decoding of from is done in a way that utilizes statistical properties learned from training data . The encoding, on the other hand, may either involve a known random Gaussian matrix , as is the case above, or it may also be learned as a part of the training procedure.

There are two statistical compressive sensing methods discussed in this paper. One is prior work that leverages the generative stage of variational autoencoders to reconstruct from  (Bora et al. 2017). In this paper, the decoding network of learned VAE creates an from a sample . This is adapted to a compressive sensing framework of recreating the best from measurement by solving the following minimization problem:

Here, is the VAE decoding mapping. The optimization is: given some measurements , we seek to find the that generates an such that, when it is compressed, best matches the measurements .

This VAE-based decompression method is used as a comparison to a new method presented in this paper, called the Uncertainty Autoencoder (UAE) which is able to optionally learn both an encoding process, the mapping of to , and a decoding process, the recovery of a reconstructed from a . It learns these encoding and decoding mappings by maximizing the mutual information between and , parameterized by encoding and decoding distributions. The objective, derived through information theoretic principles, can be written as:

Here, is an encoding distribution parameterized like the original sparse coding compression mapping , and  is a variational distribution that decodes from using a deep neural network parameterized by . This objective is maximized by drawing training data samples from what is asserted as a uniform prior over , which is simply the data itself, .

Using this objective, it is possible to derive an optimal linear encoder under a Gaussian noise assumption in the limit of infinite noise. This linear encoding, however, is not the same as PCA, which is derived under the assumption of linear decoding. UAE linear compression, instead, makes no assumptions about the nature of the decoding. The authors use this optimal linear compressor on MNIST, and use a variety of classification algorithms (k-nearest neighbors, SVMs, etc) on this low-d representation to test classification performance. They find that the UAE linear compression better separates clusters of digits than PCA. It is unclear, however, how this UAE classification performance would compare to linear compression algorithms that are known to work better for classification, such as random projections and ICA. I suspect it will not do as well. Without these comparisons, unclear what use this particular linear mapping provides.

The authors demonstrate that UAE outperforms both LASSO and VAE decoding on reconstruction of MNIST and omniglot images from compressed measurements. They implement two versions of the UAE, one that includes a trained encoding , and another where is a random Gaussian matrix, as it is for the other decoding conditions. This allows the reader to distinguish to what extent the UAE decoder does a better job at reconstructing under the same encoding as the alternative algorithms.

Most interestingly, the authors test the UAE in a transfer compressive sensing condition, where an encoder and decoder is learned on some data, say omniglot, and the decoder is re-learned using compressed measurements from different data, MNIST. In this condition, the training algorithm has no access to the test MNIST signals, but still manages to accurately recover the test signals given their compressed representations. This suggests that reasonably differently structured data may have similar optimal information-preserving linear encodings, and an encoder learned from one type of data can be utilized to create effective reconstruction mappings across a variety of data domains. The applications here may be useful.

It is unclear, however, how well these comparisons hold up in a context where traditional compressive sensing has proven to be very effective, like MRI imaging.

There are interesting parallels to be drawn between the UAE and other recent work in generative modeling and their connections to information theory. As the author’s point out, their objective function corresponds to last week’s –VAE objective function with . That is, the UAE objective written above is the same as the VAE objective minus the KL term. Though a VAE with does not actually satisfy the bound derived from the marginal distribution, and hence is not a valid ELBO, is does satisfy the bound of maximal mutual information. And as Mike derives in the post below, there is an additional connection between rate-distortion theory and the –VAE  objective. This suggests that powerful generative models can be derived from either principles of Bayesian modeling or information theory, and connections between the two are just now beginning to be explored.

 

 

 

 

Reductions in representation learning with rate-distortion theory

In lab meeting this week, we discussed unsupervised learning in the context of deep generative models, namely -variational auto-encoders (-VAEs), drawing from the original, Higgins et al. 2017 (ICLR), and its follow-up, Burgess et al. 2018. The classic VAE represents a clever approach to learning highly expressive generative models, defined by a deep neural network that transforms samples from a standard normal distribution to some distribution of interest (e.g., natural images).  Technically, VAE training seeks to maximize a lower bound on the likelihood , where defines the generative mapping from latents to data . This “evidence lower bound” (ELBO) depends on a variational approximation to the posterior, , which is also parametrized by a deep neural network (the so-called “encoder”).

A crucial drawback to the classic VAE, however, is that the learned latent representations tend to lack interpretability. The -VAE seeks to overcome this limitation by learning “disentangled” representations, in which single latents are sensitive to single generative factors in the data and relatively invariant to others (Bengio et al. 2013). I would call these “intuitively robust” — rotating an apple (orientation) shouldn’t make its latent representation any less red (color) or any less fruity (type). To overcome this challenge, -VAEs optimize a modified ELBO given by:

with and standard VAEs corresponding to . The new hyperparameter controls the optimization’s tension between maximizing the data likelihood and limiting the expressiveness of the variational posterior relative to a fixed latent prior .

Recent work has been interested in tuning the latent representations of deep generative models (Adversarial Autoencoders (Makhzani et al. 2016), InfoGANS (Chen et al. 2016), Total Correlation VAEs (Chen et al. 2019), among others), but the generalization used by -VAEs in particular looked somehow familiar to me. This is because -VAEs recapitulate the classical rate-distortion theory problem. This was observed briefly also in recent work by Alemi et al. 2018, but I would like to elaborate and show explicitly how -VAEs are reducible to a distortion-rate minimization using deep generative models.

Rate-distortion theory is a theoretical framework for lossy data compression through a noisy channel. This fundamental problem in information theory balances the minimum permissible amount of information (in bits) transmitted across the channel, the “rate”, against the corruption of the original signal, a penalty measured by a “distortion” function . Our terminology changes, but the fundamental problem is the same; I made that comparison as obvious as possible in the figure below.

Derivation. Given a dataset with a distribution , define any statistical mapping that encodes into a code . Note that is just an encoder, and together they induce a joint distribution with a marginal . The distortion-rate optimization would minimize distortion subject to a maximum rate , i.e.

Consider first the mutual information. We leverage a more tractable upper bound with

We’ve replaced the marginal induced by our choice of encoder with another distribution that makes the optimization more tractable, e.g. in the VAE. Our objective can be rewritten as

Suppose the distortion of interest is posterior density (mis)estimation, . Such a function penalizes representations from which we cannot regenerate an observed data vector through the decoding network with high probability. A typical distortion-rate problem would fix the distortion function, but we choose to learn this decoder. We can optimize the objective for each to eliminate the outer expectation over the data , fix , and recover the -VAE objective precisely:

When , our optimization prioritizes minimizing the second term (rate) over maximizing the first one (distortion). In this sense, the authors’ argument for large can be reinterpreted as an argument for higher-distortion, lower-rate codes (read: latent representations) to encourage interpretability. I edited a figure below from Alemi et al. 2018 to clarify this.

Distortion (D) vs. Rate (R) as a function of free parameters in the rate-distortion problem (and -VAEs) — the proposed method privileges solutions in the top-left quadrant (adapted from Alemi et al. 2018).

Information-theoretic hypotheses abound. Perhaps enforcing optimization in this region could discourage solutions that depend on learning an ultra-powerful decoder (VAE: generator) , in other words solutions that depend on a good code, not necessarily a good decode. Does eliminating this possibility simply make room to fish out an ad-hoc interpretable representation, or is there a more sophisticated explanation waiting to be found? We’ll see.

Machine Theory of Mind

In lab meeting last week, we read Machine Theory of Mind, a recent paper from Neil Rabinowitz and his collaborators at DeepMind & Google Brain (a trimmed version of the paper was presented at ICML 2018). Here, Theory of Mind (ToM) is broadly defined as the ability to represent the mental states of others. This paper aims to demonstrate ToM in an artificial agent. While designing & training such an agent constitutes one challenge, the authors must first devise a scenario in which ToM can be convincingly shown. Inspired by the Sally-Anne test — a classic test of ToM from developmental psychology that evaluates whether a child understands that others can hold false beliefs — the authors construct an analogous test, then train an agent to successfully pass it.

The paper is composed of a series of experiments that build in complexity to this final test. Within each experiment are three key parts. First, the environment: a simple 11×11 grid-world containing walls and 4 colored boxes that are all randomly located within each new world. Second, the agents: an individual agent belongs to a particular “species” according to its policy for acting within an environment. Agents can behave randomly, algorithmically, or with a learned policy (via deep RL). The trajectory of a particular agent within a particular environment constitutes an episode. Reward within an episode is generally maximized by navigating to a box of a particular color as fast as possible. However, limitations on the sightedness and statefulness of the agents, as well as the inclusion of more complex subgoals, are adjusted per the needs of each experiment. Finally, the observer: a meta-learning agent, called ToMnet, that parses the episodes of many agents in many environments so as to learn a prior over the behavior of an agent species. At test time, ToMnet uses a novel agent’s recent episodes & its trajectory on a current episode thus far to infer a posterior and make predictions regarding the agent’s future behavior.

From Figure 4 in the paper. (a) An example environment. The red arrows represent the trajectory of a goal-driven agent on a previous episode. (b) A new environment, but the same agent as in (a). Using a prior learned over the agent’s species (e.g., agents of this species seek to consume a box of a specific color) in combination with this agent’s past episodes (e.g., this agent consumed a green box), ToMnet is tasked with predicting the agent’s future behavior. (c) For the new environment in (b), ToMnet outputs the next predicted action (go right) and the predicted color of the box that will eventually be consumed (green). (d) ToMnet also predicts the agent’s successor representation.

To probe ToM in ToMnet, the authors introduce a species of agent with both a limited field of view and a subgoal. For example, an agent that can only see the squares adjacent to it must first navigate to a “star” in the grid-world before finally navigating to the blue box to achieve maximum reward. In certain environments, the agent passes the blue box early in its initial search and so knows directly where to go after finding the star, even if the blue box is not visible to the agent from the star’s location. The test comes when the experimenter now swaps the locations of the boxes while the agent is on the star and the boxes are out of view. While the agent is blind to the swap, ToMnet is not. And so, the analogous Sally-Anne test arises: Will ToMnet not recognize that the swap occurred outside of the agent’s field of view, and thus mistakenly predict that it will move toward the new location of the blue box? Or, will ToMnet recognize that the agent maintains the false belief that no swap has occurred, and thus correctly predict that it will move toward the old location of the blue box?

ToMnet predicts behavior reflecting the agent’s false belief, successfully passing the test. Importantly, this finding is supplemented with results that show that ToMnet is sensitive to how different fields of view make an agent “differentially vulnerable to acquire false beliefs,” and that ToMnet still passes the test even if it had never seen swap events during training. Thus, ToMnet “learns that agents can act based on false beliefs,” providing a compelling proof-of-concept for Machine Theory of Mind.

Insights on representational similarity in neural networks with canonical correlation

For this week’s journal club, we covered “Insights on representational similarity in neural networks with canonical correlation” by Morcos, Raghu, and Bengio, NeurIPS, 2018.  To date, many different convolutional neural networks (CNNs) have been proposed to tackle the object recognition problem, including Inception (Szegedy et al., 2015), ResNet (He et al., 2016), and VGG (Simonyan and Zisserman, 2015). These networks have vastly different architectures but all achieve high accuracy. How can this be the case? One possibility is that although the architectures vary, the representations (i.e., the way these networks encode information about the objects of natural images) are very similar. 

To test this, we first need a metric of similarity. One approach has been “representation similarity analysis” (RSA) (Kriegskorte et al., 2008) which relies on distance matrices to test if two representations are similar. One potential problem with RSA is that some dimensions of the representations may be “noisy” (i.e., dimensions that do not pertain to encoding the input information). For example, during training, some dimensions of the activity of CNN neurons may vary substantially across epochs but are not relevant to encoding object information. These dimensions could mask the signal of relevant dimensions when analyzing a distance matrix. 

One way to avoid this is to try to directly identify the relevant dimensions, allowing us to ignore the noisy dimensions. The authors relied on an old but trusted method called canonical correlation analysis (CCA), which was developed way back in the 1930s (Hotelling, 1936)! CCA has been a handy tool in computational neuroscience, relating the activity of neurons across two populations (Semedo et al., 2014) as well as relating population activity to the output of model neurons (Susillo et al., 2015). Newer methods have been developed that are more appropriate for various problems. These include partial least squares (Höskuldsson, 1988), kernel CCA (Hardoon et al., 2004), as well as a method I developed for my own work called distance covariance analysis (DCA) (Cowley et al., 2017).  The common thread among all of these methods is that they identify dimensions that encode similar information among two or more datasets.

Overview of CCA. CCA is a close relative to linear regression, but whereas linear regression aims at prediction, CCA focuses on correlation—and thus is most suitable for cases in which the investigator seeks intuition of the data.  Given two datasets (e.g., , both centered, where is the number of samples), CCA seeks to identify a pair of dimensions such that the Pearson’s correlation between the projections is the largest. In other words, CCA identifies linear combinations of the variables in that are the most linearly-related. CCA need not stop there—it can identify pairs of dimensions that monotonically decrease in correlation. In this way, we can ignore the dimensions with the smallest correlations (which likely are spurious). One fun fact about CCA is that any two identified dimensions in are uncorrelated: (and the same for ). This is different from PCA, whose identified dimensions are both uncorrelated and orthogonal.  The uncorrelatedness of CCA dimensions ensures that we do not include dimensions that contain redundant information. (Implementation details: CCA is solved with singular-value decomposition, but be sure to use a regularized form akin to ridge regression—it was unclear if the authors used regularization). 

Figure 1. Generalizing networks converge to more similar solutions than memorizing networks.

Onto the results. The authors proposed a distance metric of CCA to uncover some intuitive characteristics about deep neural networks. First, they found that different initializations of generalizing networks (i.e., networks trained on labeled natural images) were more similar than different initializations of memorizing networks (i.e., networks trained on the same dataset with randomly-shuffled labels). This is expected, as natural labels likely put a constraint on generalizing networks. Interestingly, when comparing generalizing and memorizing networks (Fig. 1, yellow line, ‘Inter’), they found that generalizing and memorizing networks were as similar as different memorizing networks trained on the same fixed dataset. This suggests that overfitted networks converge on very different solutions for the same problem. Also interesting was that earlier layers of both generalizing and memorizing networks seem to converge on similar solutions, while the later layers diverged. This suggests that earlier layers rely more on the structure of natural images while the later layers rely more on the structure of the labels. Second, they found that wider networks (i.e., networks with more filters per layer) converge to more similar solutions than those of narrower networks.  They argue that this supports the “lottery-ticket” hypothesis that wider networks are more likely to have a sub-network that fits the desired function.  Finally, they found that networks trained with different initializations and learning rates on the same problem converge to different groups of solutions. This highlights the need to try different initializations when training neural networks.

This paper left me thinking a lot about representation in the visual cortex of the brain. Does visual cortical population activity have stable and “noisy” dimensions?  If we reduced the number of visual cortical neurons per visual cortical area (either via lesion or pharmacological intervention) in a developing animal, would these animals have severe perceptual deficits (i.e., their visual system did not have the right lottery ticket when developing)?  Lastly, it seems plausible that humans start out with different initializations of their visual cortices—does that suggest different humans have converged on different solutions to solving visual perception?  If so, it suggests that inter-subject variability may be larger than previously thought.

The Loss-Calibrated Bayesian

By Farhan Damani

In lab meeting this week, we discussed loss-calibrated approximate inference in the context of Bayesian decision theory (Lacoste-Julien et. al. 2011, Cobb et. al. 2018). For many applications, the cost of an incorrect prediction can vary depending on the nature of the mistake. Suppose you are in charge of controlling a nuclear power plant with an unknown temperature . We observe indirect measurements of the temperature , and we use Bayesian inference to infer a posterior distribution over the temperature given the observations . The plant is in danger of over-heating and as the operator, you can either keep the plant running or shut it down. Keeping the plant running while the plant’s temperature exceeds a critical threshold will cause a nuclear meltdown, incurring a huge loss while shutting off the plant for benign temperatures incurs a minor loss . 

In figure 1 we observe the true posterior is multi-modal. Our suite of approximate inference techniques characterize general properties of the posterior, attempting to match either the first or second moment of . Both strategies underestimate the posterior mass for the safety-critical region. Instead, the dash-dotted line, while failing to characterize typical properties of the posterior, results in the same decision as the true posterior by optimizing for task-specific utility. The point is the “best” approximate posterior is subjective, and therefore, we should tailor our inferential resources to find an approximation that is well suited for the decision task at hand.

Bayesian decision theory extends the Bayesian paradigm by including a task-specific utility function , which tells us the utility of taking action when the world is in state . According to this view, the optimal action minimizes the posterior risk: . Typically, this is computed using a 2-step procedure. First approximate the posterior with a and then minimize the risk under . This approach, however, assumes our approximate measures properties of the posterior that we care about. This by definition requires our utility function, so therefore, we should jointly optimize the approximate posterior with the action that minimizes the posterior risk. Cobb et. al. 2018 show how to derive a variational lower bound that depends on a task-specific utility function. In their setup, they show that minimizing the KL divergence between an approximate posterior q and a calibrated posterior scaled by the utility function results in the standard ELBO loss plus an additional utility-dependent regularization term. This formulation is amenable to stochastic optimization, allowing for the practical deployment of this framework to supervised learning.

An orderly single-trial organization of population dynamics in premotor cortex predicts behavioral variability

This week we read some new work from Shaul Druckmann and Karel Svoboda’s groups (https://www.biorxiv.org/content/early/2018/07/25/376830). They analyzed simultaneously recorded activity from the anterior lateral motor cortex (ALM; perhaps homologous to a premotor area in primates) from mice performing a delayed discrimination task (either a somatosensory pole detection task or an auditory tone discrimination task). They analyzed 55 sessions with 6-31 units on each session. Given the strong task epoch dependent responsiveness of most cells in the population, they fit a switching linear dynamical system (sLDS) to the data using expectation-maximazation. However, in their model, the switch times were dictated by the task structure, making the model significantly easier to fit than a sLDS with unconstrained switch times. They called their model a epoch-dependent linear dynamical system (EDLDS).

They used leave-one-neuron-out cross validation (i.e. compute the posterior on test trials without including one neuron’s activity, and then predict that neuron’s activity from the posterior) to test the model fit and found that it often fit the data about as well a sLDS that could flexibly assign the timing of the same number of switch events and significantly outperformed Gaussian process factor analysis.

The model defines a low-dimensional latent space to which they apply several analyses. First, they applied linear discriminate analysis (LDA) to decode the animal’s choice on each trial and show that it outperforms LDA applied to the activity of the full neural population, even when regularization is included.

Next, they applied principal components analysis (PCA) to the latent activity and the full neural population activity to visualize the dominant temporal trajectories within each space. PC projections of the full population activity showed sharp temporal transitions between task epochs and a random spatial ordering across trials, while PC projections of the latent activity showed smooth temporal transitions and strongly ordered dynamics.

They quantified the “orderliness” of each representation by computing the consistency of the trial-ranked value of the LDA projection across time to confirm greater orderliness within the latent space than the full neural activity. They also found that decode analyses to previous trial outcome or choice on error trials using the latent activity outperformed the same analyses applied to the full neural activity.

In summary, the dynamical nature of the EDLDS provides a smooth, de-noised portrait of the temporal dynamics present in the data but that might not easily reveal itself with standard analyses.