state-space models | Pillow Lab Blog

This week I followed up on the previous week’s meeting about state-space models with a tutorial on Kalman filtering / smoothing. We started with three Gaussian “fun facts” about linear transformations of Gaussian random variables and products of Gaussian densities. Then we derived the Kalman filtering equations, the EM algorithm, and discussed a simple implementation of Kalman smoothing using sparse matrices and the “backslash” operator in matlab.

Here’s how to do Kalman smoothing in one line of matlab:
Xmap = (Qinv + speye(nsamps) / varY) \ (Y / varY + Qinv * muX);
where the latent variable X has prior mean muX and inverse covariance Qinv, and Y | X is Gaussian with mean X and variance varY * I. Note Qinv is tri-diagonal and can be formed with a single call to “spdiags”.

Today I presented a paper from Liam’s group: “A new look at state-space models for neural data”, Paninski et al, JCNS 2009

The paper presents a high-level overview of state-space models for neural data, with an emphasis on statistical inference methods. The basic setup of these models is the following:

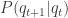
• Latent variable $Q$ defined by dynamics distribution: $P(q_{t+1}|q_t)$
• Observed variable $Y$ defined by observation distribution: $P(y_t | q_t)$ .

These two ingredients ensure that the joint probability of latents and observed variables is
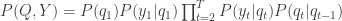$P(Q,Y) = P(q_1 ) P(y_1|q_1) \prod_{t=2}^T P(y_t | q_t) P(q_{t}|q_{t-1})$ .
A variety of applications are illustrated (e.g., $Q$ = common input noise; $Y$ = multi-neuron spike trains).

The two problems we’re interested in solving, in general, are:
(1) Filtering / Smoothing: inferring $Q$ from noisy observations $Y$ , given the model parameters $\theta$ .
(2) Parameter Fitting: inferring $\theta$ from observations $Y$ .

The “standard” approach to these problems involves: (1) recursive approximate inference methods that involve updating a Gaussian approximation to $P(q_t|Y)$ using its first two moments; and (2) Expectation-Maximization (EM) for inferring $\theta$ . 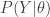By contrast, this paper emphasizes: (1) exact maximization for $Q$ , which is tractable in $O(T)$ via Newton’s Method, due to the banded nature of the Hessian; and (2) direct inference for $\theta$ using the Laplace approximation to $P(Y|\theta)$ . When the dynamics are linear and the noise is Gaussian, the two methods are exactly the same (since a Gaussian’s maximum is the same as its mean; the forward and backward recursions in Kalman Filtering/Smoothing are the same set of operations needed by Newton’s method). But for non-Gaussian noise or non-linear dynamics, the latter method may (the paper argues) provide much more accurate answers with approximately the same computational cost.

Key ideas of the paper are:

exact maximization of a log-concave posterior
$O(T)$ computational cost, due to sparse (tridiagonal or banded) Hessian.
the Laplace approximation (Gaussian approximation to the posterior using its maximum and second-derivative matrix), which is (more likely to be) justified for log-concave posteriors
log-boundary method for constrained problems (which preserves sparsity)

Next week: we’ll do a basic tutorial on Kalman Filtering / Smoothing (and perhaps, EM).