Bayesian inference for Poisson-GLM with Laplace prior

During the last lab meeting, we talked about using expectation propagation (EP), an approximate Bayesian inference method, to fit generalized linear models (Poisson-GLMs) under Gaussian and Laplace (or exponential) priors on the filter coefficients. Both priors give rise to log-concave posteriors, and the Laplace prior has the useful property that the MAP estimate is often sparse (i.e., many weights are exactly zero).  EP attempts to find the posterior mean, which is not (ever) sparse, however.

Bayesian inference under a Laplace prior is quite challenging. Unfortunately, our best friend the Laplace approximation is intractable, since the prior is non-differentiable at zero.

Lab meeting 06/25/12

In the paper “Automating the design of informative sequences of sensory stimuli” (by Lewi, Schneider, Woolley & Paninski, JCNS 11), the authors developed an algorithm to adaptively select stimuli during real-time sensory neurophysiology experiments. Given a set of already recorded responses, their algorithm determines which stimuli to present next so that the recorded data can provide as much information about the structure of the receptive field as possible.

Unlike their previous paper (NC 09), in this paper, they focused on the selection of informative stimulus “sequences” (or batches) to keep temporal or other types of correlations in stimuli.  They denoted the length of sequence by b and talked about two cases, where b is some finite number and b goes to infinity. In both cases, selecting a sequence of stimuli turned out to be computationally challenging, so they developed lower bounds using Jensen’s inequality when computing the expected information gain. When b goes to infinity, they restricted the stimulus distribution to Gaussian to make the high dimensional optimization problem (over stimulus distribution) tractable.  They tested the developed algorithm to real songbird auditory responses, and showed that the chosen stimulus sequences decreased the error significantly faster than i.i.d. experimental designs.

Lab meeting 7/28/11

Last Thursday we discussed how to fit psychophysical reverse correlation kernels using logistic regression, regularized by using an L1 prior over a basis vectors defined by a Laplacian pyramid (Mineault et al 2009). In psychophysical reverse correlation, a signal is embedded in noise and the observer’s choices are correlated with the fluctuations in the noise, revealing the underlying template the observer is using to do the task. Traditionally this is done by sorting the choices — as hits, misses, false alarms correct rejects — and averaging across the noise frames for each set of choices, then subtracting the average noise frame for the misses and correct rejects from the hits and false alarms. The resulting kernel is the size (space x space x time) of the stimulus, which becomes high-dimensional fast and therefore requires a lot of trials to get enough data. As an alternative, one can use maximum likelihood to do logistic regression and apply priors to reduce the number of trials required:

maximize 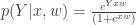, where Y is the observer’s responses, x is a matrix of the stimulus (trials x stimulus vector) augmented by a column of ones (for the observer’s bias), and w is the observer’s kernel (size = [1 x(1,:)]). Using a sparse prior (L1 norm) over a set of smooth basis (defined by a laplacian pyramid) reduces the number of trials required to fit the kernel while adding only one hyperparameter. The authors use simulations and real psychophysical data to fit an observer’s psychophysical kernel and their code is available here.